آموزش ریاضیات برای یادگیری ماشین

یادگیری ماشین یکی از شاخه‌های هوش مصنوعی است که در آن کامپیوترها با استفاده از الگوریتم‌های خاص، قادر به یادگیری از داده‌ها هستند و بر اساس آن‌ها، پیش‌بینی‌هایی انجام می‌دهند یا تصمیم‌هایی می‌گیرند. پایتون یک زبان برنامه‌نویسی بسیار قدرتمند و پویا است که برای برنامه‌نویسی کاربردی، علم داده، هوش مصنوعی، تحلیل داده، وب، بازی‌ها و بسیاری از کاربردهای دیگر استفاده می‌شود. به طور کلی، پایتون به دلیل سادگی و آسانی در یادگیری، خوانایی کد و امکانات بسیاری که در آن وجود دارد، بسیار محبوب است.

 

 

اهمیت یادگیری ریاضی برای یادگیری ماشین و پیاده‌سازی در پایتون چیست؟

ریاضی هسته اصلی طراحی الگوریتم های ML است که می تواند به طور خودکار از داده ها یاد بگیرد و پیش بینی کند. بنابراین، درک ریاضی قبل از ورود به مبحث الگوریتم‌های ML بسیار مهم است. یادگیری ریاضی یکی از اصولی‌ترین و ضروری‌ترین بخش‌های یادگیری ماشین است. در واقع، ریاضیات در تمامی الگوریتم‌های ماشینی به کار می‌رود و برای پیاده‌سازی این الگوریتم‌ها در پایتون نیز باید با اصول ریاضی آشنا باشید. یکی از مهم‌ترین مفاهیم ریاضی در یادگیری ماشین، آمار و احتمالات است.

یادگیری ماشین(machine learning) آخرین مورد از تلاش‌ها برای تقطیر دانش و استدلال انسان به شکلی است که برای ساخت ماشین‌ها و سیستم‌های خودکار مهندسی مناسب باشد. با فراگیرتر شدن یادگیری ماشین و استفاده از بسته‌های نرم‌افزاری آن، طبیعی و مطلوب است که جزئیات فنی سطح پایین، از نظر دانشجو پنهان شود. با این حال، این خطر وجود دارد که یک متخصص از تصمیمات طراحی و در نتیجه محدودیت‌های الگوریتم‌های یادگیری ماشین بی‌اطلاع شود.

یادگیری ماشینی بر پایه زبان ریاضیات است تا مفاهیمی را بیان کند که به طور شهودی بدیهی به نظر می رسند اما رسمی کردن(formalize) آنها به طرز شگفت انگیزی دشوار است. هنگامی که به درستی رسمی شد، می‌توانیم در مورد کاری که می‌خواهیم بکنیم، بینشی به دست آوریم. یکی از شکایات رایج دانشجویان ریاضیات در سراسر جهان این است که به نظر می رسد موضوعات تحت پوشش، ارتباط کمی با مسائل عملی دارند. ما معتقدیم که یادگیری ماشین انگیزه ای آشکار و مستقیم برای مردم برای یادگیری ریاضی است. در لینک زیر ویدیو آموزش ریاضیات برای هوش‌مصنوعی و یادگیری ماشین به زبان فارسی در یوتیوب را مشاهده می کنید.

 

🔗 https://www.youtube.com/playlist?list=PLe_DUrcBPdbIRye6Dw_UdhR8a7Zqvb_BA

 

مروری بر بخش اول کتاب ریاضیات برای یادگیری ماشین (Mathematics for Machine Learning) که در سال ۲۰۲۰ برای اولین بار به چاپ رسیده است. این کتاب توسط سه نفر نوشته شده است:

A. Aldo Faisal
Cheng Soon Ong
Marc Peter Deisenroth

همانطور که در وبسایت کتاب ذکر شده است، این کتاب تکنیک های پیشرفته یادگیری ماشین را پوشش نمی دهد، چون کتاب های بسیاری در این مورد وجود دارد. در عوض، هدف این کتاب، ارائه مهارت های ریاضی لازم برای خواندن کتاب هایی است که به تکنیک های پیشرفته یادگیری ماشین می پردازند.

 

فهرست بخش اول کتاب

Part I: Mathematical Foundations

۱- Introduction and Motivation

۲- Linear Algebra

۳- Analytic Geometry

۴- Matrix Decompositions

۵- Vector Calculus

۶- Probability and Distribution

۷- Continuous Optimization

 

 

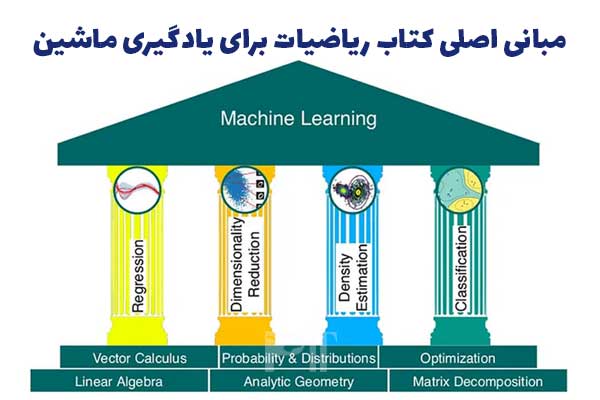
بخش اول کتاب شامل ۷ فصل می باشد که آنها را تک تک مرور می کنیم:

فصل اول: مقدمه و انگیزه
فصل اول کتاب «مقدمه و انگیزه» نام دارد و همانطور که از اسم آن مشخص است، کتاب را معرفی می کند و کلمات و مفاهیمی را تعریف می کند که در کتاب قرار است بررسی شوند. همچنین دو روش برای مطالعه این کتاب پیشنهاد می دهد:

استراتژی جز به کل یا پایین به بالا «ایجاد مفاهیم از سطح بنیادی تا پیشرفته»
استراتژی کل به جز یا بالا به پایین «کند و کاو و شکستن مساله از نیازهای عملی به نیازمندی های ابتدایی تر».
فصل های ۲ و ۳ و ۴ به حوزه جبر خطی می پردازد اما نویسندگان ترجیح داده اند که آن را به سه موضوع تقسیم کنند: جبر خطی (مفاهیم «پایه» و «عام»)، هندسه تحلیلی (شهودهای هندسی) و تجزیه ماتریس (برخی عملیات ریاضی و خودِ تجزیه ماتریس). فکر می کنم دلیل این مساله این است که به دنبال این بودند که هر فصل مختصر، مفید و ماژولار باشد، نه اینکه یک فصل جامع و عظیم باشد.

 

 

فصل دوم: جبر خطی

 

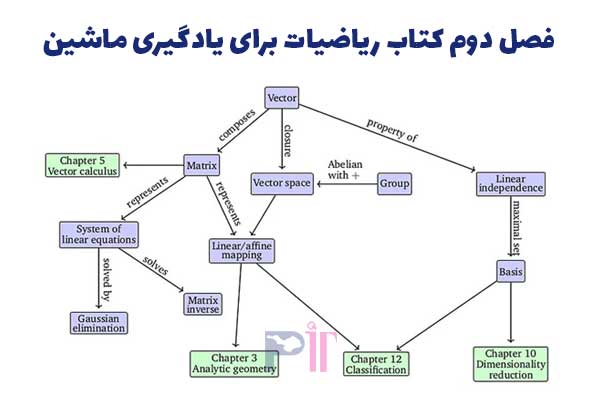
در فصل دو «جبر خطی»، کتاب با مفاهیم ابتدایی ریاضیات سطح دبیرستان (دوره متوسطه دوم) شروع می کند (دستگاه معادلات خطی، ماتریس ها، شکل سطری پلکانی، تکنیک حذف گاوسی، شبه وارون مور-پنروز) و بعد سرا مفاهیمی مجرد و انتراعی تر می رود (مثل زیرفضا و فضای برداری، استقلال خطی، همریختی و نگاشت آفین).

این فصل برای مرور و به یاد آوردن ایده ها و مفاهیم قدیمی، بسیار کامل و مفید بود. تعریف ها و مفاهیم ریاضی به طور کلی، به خوبی تعریف شده اند و به حد کافی پیچیده و دقیق توضیح داده شده اند.

به علاوه، هر زیرفصل هم مثال هایی تصویری دارد که باعث می شود درک مساله ساده تر شود. این تصاویر همچنین برای درک تجریدها بسیار عالی هستند. همچنین پیاده سازی کامپیوتری / محاسباتی و عملکرد این تکنیک ها به شکل مفصل شرح داده شده اند.

همچنین از این مساله خیلی خوشم آمد که ویژگی های خیلی مهم و جالب هم توضیح داده شده اند (به عنوان مثال می توانید دنبال درجه یا رتبه بگردید). در این فصل، چند تمرین خوب وجود دارد (که حل کردن آن ها، نیازمند این هستند که درک خوبی از مفاهیم آموخته شده داشته باشید)، اما چند تمرین هم خسته کننده و تکراری بودند (حاصلضرب ماتریس، حل کردن دستگاه خطی و به کارگیری مستقیم تکنیک ها).

 

فصل سوم: هندسه تحلیلی

 

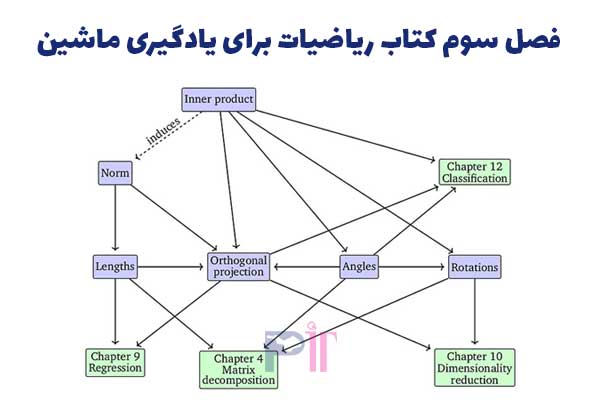
در فصل سوم کتاب با عنوان «هندسه تحلیلی»، از مفاهیم انتزاعی/تجریدی فصل قبل برای تعریف کردن المان های هندسی استفاده می شود: نُرم، ضرب داخلی، طول و فاصله، زاویه و تعامد، تصویر (پروجکشن) و دوران. مثل فصل قبل، این فصل هم به خوبی ایده ها را شرح داده است و تا حد کافی فرمولی شده و کلی است.

در هندسه تحلیلی، مهم است که مفاهیم را به شکل کلی آموزش دهیم تا مخاطب، دیدگاهی محدود نسبت به فضای اقلیدسی پیدا نکند (با آنکه تصویرسازی ها در آن انجام می شود). این کتاب از این نظر بسیار شفاف و واضح است، که نکته بسیار مثبتی است. به طور مثال، تمام عملیات ابتدای در فضای دوبعدی / سه بعدی شرح داده شده اند، سپس به فضای n بعدی تعمیم داده شده اند (با دوران ها!).

اینجا هم تصاویر و نمودارها برای تصویرسازی و بصری سازی تمام ایده های هندسی، بسیار مفید هستند. به علاوه، من فکر می کنم که مهم ترین ماتریس ها برای یادگیری ماشین در حوزه هندسه تحلیلی به شکل مفصل شرح داده شده اند، همچون ماتریس های متقارن، (نیمه) معین مثبت و متعامد. این کتاب همچنین ضرب داخلی برای توابع را توضیح داده، که در دامنه پیوسته بسیار مهم است.

البته چند نکته منفی هم در این فصل پیدا کردم. فرآیند گرام اشمیت به شکل سطحی مطرح شده است. من فکر می کنم که برای روش هایی مهم در یادگیری ماشینی مرسوم، مهم است که ایده تصویر کردن (پروجکشن) کامل آموزش داده شود.

به علاوه، گاهی اوقات فکر می کنم که تصاویر و نمودارها، فاصله زیادی با بخشی از متن دارند که در مورد آن هاست. این شاید نکته مهمی به نظر نرسد، اما به نظرم خواندن کتاب را سخت تر کرده است. در نهایت، تمرین ها اینجا هم طبق رویکرد فصل قبل نوشته شده اند، البته حجم و تعداد آن ها خیلی کمتر است.

 

فصل چهارم: تجزیه ماتریس

 

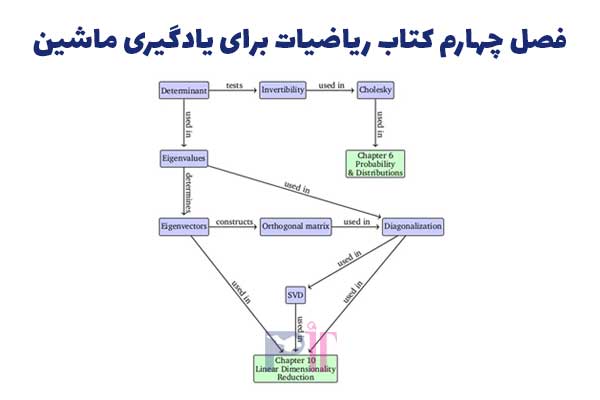
فصل چهارم «تجزیه ماتریس» نام دارد، که برای حوزه یادگیری ماشین (ML) بسیار قابل توجه و مهم است. ابتدا با مفاهیم سطح دبیرستان شروع می شود (اثر، دترمینان و وارون پذیری) و سپس سراغ ایده های قدرتمندتر می رود (تجزیه ویژه/قطری سازی، تجزیه مقدارهای منفرد یا SVD، تجزیه چولیسکی و تقریب رتبه پایین).

این فصل، سطح کیفی مشابهی با دو فصل قبلی در مورد جبر خطی دارد (از نظر فرمولی بودن، درک ساده، تصویرسازی ها، ویژگی های خوب و تمرینات)، ولی یک ویژگی خیلی عالی دیگر هم دارد. چند مثال بصری و تصویرسازی شده از کاربردهایی در دنیای واقعی دارد («طیف ویژه یک شبکه عصبی بیولوژیکی»، رتبه صفحه یا پیج رنک گوگل: صفحات وب به عنوان بردارویژه» و «پیدا کردن ساختار در رتبه بندی فیلم ها و مصرف کنندگان»).

این بسیار جالب است که می بینیم این ایده های کاملا تجریدی و انتزاعی را می توان به شکل مستقیم روی مشکلات واقعی، با یک مدلسازی ریاضیاتی آگاه بخش، پیاده سازی کرد.

 

فصل پنجم: حساب برداری

 

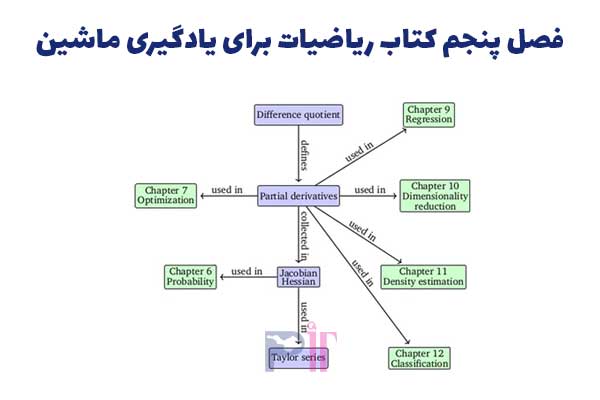
فصل پنجم در مورد حساب برداری است و به نظر من، تمرکز زیادی روی نظریه بهینه سازی پایه برای یادگیری ماشین دارد. این فصل به این موارد می پردازد: مشتقات (جزئی)، بسط یا سری تیلور، قاعده زنجیره ای، گرادیان، حساب ماتریس ها، پس انتشار یا انتشار معکوس و مشتق گیری اتوماتیک و کمی هم مشتق مراتب بالاتر و خطی سازی. اکثر این ایده ها و مفاهیم را می توانید در هر کتابی با موضوع حسابان پیدا کنید.

اما مزیت عالی این کتاب، تاکید آن روی عملیات حسابان ماتریسی است (که زیاد رایج نیست) و همچنین حوزه شبکه های عصبی (عمیق). در نتیجه من فکر می کنم خواندن این فصل حداقل برای کسی که در حوزه یادگیری عمیق تازه کار است، مفید است. همچنین خوب است که مثالی از گرادیان در اتلاف کمترین مربعات هم اینجا وجود دارد.

این فصل به اندازه فصول قبلی، دارای فرمول های ریاضی نیست (به طور مثال، تعریف دقیقی از پیوستگی یا دیفرانسیل پذیری، مفاهیم توپولوژی و برخی اثبات ها وجود ندارد). همچنین اصلا به انتگرال اشاره نشده است. اما همان حس مختصر مفید بودن کتاب را حفظ کرده است و چنین فرمول هایی که گفتم، شاید خارج از مبحث این کتاب به حساب آید.

اینجا برای من، مثال های تصویری و بصری سازی شده، یک مقداری بیش از حد عظیم بودند و گاهی اوقات شفاف و قابل فهم نیستند. به نظر من، مسائلِ شهودی مفاهیم و ایده های مطرح شده در این فصل، به خوبی به خواننده کتاب ارائه نشده اند (برخلاف فصول پیشین)، فقط چند عملیات به شکل توصیفی ارائه شده است.

در نهایت، به نظر من در بخش مشتق گیری اتوماتیک (Automatic Differentiation)، «دیدگاه علوم کامپیوتری» خیلی لحاظ نشده است. مثلا شاید اگر ایده گراف کامپیوتری/محاسباتی بهتر تصویرسازی شده بود (به خصوص در مثال) و برخی ایده های ابتدایی پیاده سازی بهتر نمایش داده شوند، این بخش از کتاب غنی تر می شود. در نهایت، تمرینات موجود در این بخش به نظر من با به کارگیری مستقیم عملیات مشتق، بیشتر حالت «مکانیکی» دارند.

 

فصل ششم: توزیع احتمال

 

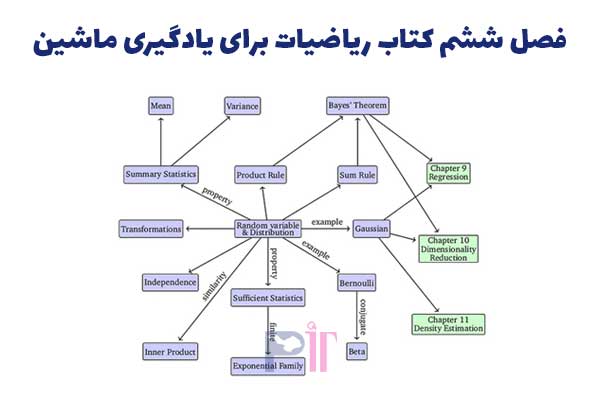
موضوعات اصلی که در این فصل مطرح شده اند عبارتند از: آمار و احتمالات، متغیرهای تصادفی، توزیع پیوسته و گسسته، قضیه بیز، آمار خلاصه، استقلال آماری، توزیع گاوسی، تزویج (conjugacy)، تغییر متغیرها. همانطور که در این نقشه ذهنی می بینیم، این فصل موضوعات زیادی را پوشش می دهد و نکات مثبت زیادی هم دارد. شیوه شرح مفصل متغیرهای تصادفی، عالی است.

به علاوه، ارتباط بین متغیرهای تصادفی و جبر خطی (هندسه تولید شده توسط ضرب داخلی کوواریانس) بسیار جالب است. یک ایده هیجان انگیز دیگر که اینجا مفصل شرح داده شده، «توپولوژی» توزیع هاست (حوزه مانیفولدهای آماری)، که پاسخی است به این سوال: «چرا ما به عنوان معیار تشابه، از واگرایی کولبک-لیبلر به جای فاصله اقلیدسی استفاده می کنیم؟».

این کتاب همچنین توزیع گاوسی را بسیار خوب و به شکل مفصل توضیح می دهد. به طور کلی این فصل، منبعی عالی برای الگوریتم های پایه و مرسوم یادگیری ماشین است. اگر بخواهم پیشنهادی برای بهتر شدن این فصل داشته باشم، بهتر بود که در بخش قضیه بیز، توضیحات بصری و مثال های بیشتری قرار می گرفت. در بخش تزویج (conjugacy) هم همینطور، این بخش به نظر من زیاد واضح و قابل درک نیست.

به علاوه، چند موضوع مهم هم هستند که این کتاب به آن ها نپرداخته (حداقل در بخش مسائل بنیادی): تست های آماری، قضیه حد مرکزی، فاصله آماری (در این کتاب فقط به واگرایی کولبک-لیبلر اشاره شده که بالاتر ذکر کردم)، بوت استرپینگ، بازه اطمینان و … . من فکر می کنم این موضوعات، همه بسیار مهم هستند، به ویژه در زمینه یادگیری تقویتی (Reinforcement Learning) و تحقیقات کلی یادگیری ماشین (ML).

 

فصل هفتم: بهینه سازی پیوسته

 

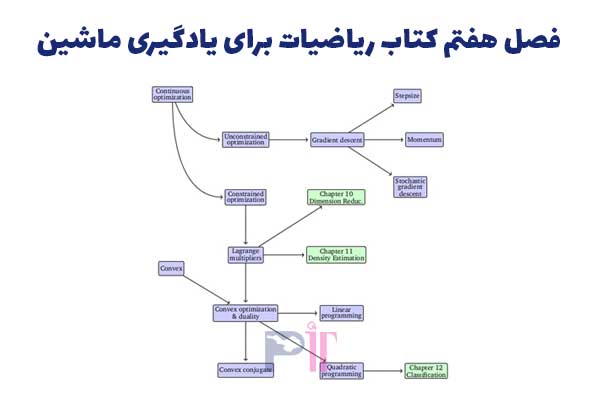
فصل آخرِ بنیان های ریاضی، به بهینه سازی پیوسته پرداخته است. به نظر من خیلی خوب است که این موضوع در یادگیری ماشین، به موضوعی ضروری تبدیل شود، با آنکه این موضوع معمولا در دانشگاه تدریس نمی شود (یا آنکه به شکلی سطحی، در کلاس های حسابان مطرح می شود). این بخش به این موضوعات می پردازد:

کاهش گرادیان، تکانه، بهینه سازی مقید (با ضرایب لاگرانژ)، بهینه سازی محدب، برنامه نویسی خطی/مربعی و تبدیل لژاندر-فنشل (و مزدوج محدب).

از نظر بهینه سازی بدون محدودیت (نامقید)، اینجا تمرکز روی بهینه سازی گرادیان است (که در حوزه شبکه های عصبی، بسیار مشهور است). این بخش های کتاب، روی بخش های خاصی از بهینه سازی متمرکز است، که با تحلیل در مورد بهره وری محاسباتی در حافظه/زمان و تصادفی بودن از نظر ابعاد batch (دسته) همراه شده است.

این بخش به طور کلی، مرزی بین ریاضی و نظریه یادگیری ماشین است (که یعنی شما می توانید این مفاهیم و ایده ها را در کتاب های یادگیری ماشین/یادگیری عمیق نیز پیدا کنید).

 

 

خلاصه نهایی

در حوزه یادگیری ماشین، ریاضیات نقش بسیار مهمی ایفا می‌کند. این حوزه نیازمند ابزارهای ریاضیاتی پیچیده است که به تحلیل، مدل‌سازی، و بهبود الگوریتم‌ها کمک کند. مفاهیم اساسی مانند جبر خطی، احتمالات و آمار، تجزیه و تحلیل عددی، و هندسه تحلیلی اساس ایجاد مدل‌های یادگیری ماشین را فراهم می‌کنند.

در مسائل کلاسیک یادگیری ماشین، ماتریس‌ها و بردارها برای نمایش داده‌ها و پارامترها به کار می‌روند. توابع ریاضی برای تعریف مدل‌ها و ارزیابی عملکرد آن‌ها بسیار حائز اهمیت هستند. همچنین، مفاهیم احتمالات و آمار در تجزیه و تحلیل داده‌ها و اعتبارسنجی مدل‌ها اساسی هستند.

به طور کلی، بدون استفاده از ریاضیات، امکان توسعه و بهینه‌سازی الگوریتم‌ها و مدل‌های یادگیری ماشین با دقت و کارایی بالا کاهش می‌یابد. استفاده از این اصول ریاضیاتی باعث پیشرفت و نوآوری در حوزه یادگیری ماشین می‌شود.

علاوه بر این، تحقیقات در حوزه ریاضیات برای پیشرفت در روش‌های پیشرفته‌تر یادگیری ماشین اساسی است. مفاهیمی چون بهینه‌سازی، تئوری اطلاعات، و یادگیری تقویتی نشان از تعامل عمیق میان ریاضیات و یادگیری ماشین دارند. بهینه‌سازی الگوریتم‌ها و توابع هدف به کمک محاسبات ریاضیاتی انجام می‌شود تا به دقت بیشتر و سرعت بهتر در آموزش مدل‌ها دست یافته شود.

از سوی دیگر، تئوری اطلاعات نقش مهمی در تحلیل ویژگی‌های مختلف داده‌ها و مدل‌ها دارد و به ما کمک می‌کند تا اطلاعات مهمترین ویژگی‌ها را در داده‌ها شناسایی کنیم. به این ترتیب، ریاضیات نه تنها به عنوان ابزاری برای پیاده‌سازی مدل‌ها، بلکه به عنوان یک زبان تحلیلی برای درک عمیقتر رفتارهای یادگیری ماشین مطرح می‌شود.

 

دانلود کتاب ریاضیات برای یادگیری ماشین به زبان انگلیسی